Horizon graf pro časové řady

11/2/2017 ⟶ vizualizace

Horizon graf je jednou z ostudně nedoceněných vizualizačních metod, které se snaží poprat s potížemi při analýze a zobrazování mnoha časových řad najednou — ať už jde o počasí, nezaměstnanost nebo třeba vývoj hodnoty akcií. Kdykoliv pracujete s časovými řadami a dostanete se do bodu, kdy je výstupem statický liniový graf s více než pěti spojnicemi, je ten správný čas zamyslet se nad vhodnější formou grafického zobrazení. Variant je několik: small multiples, braided grafy nebo horizon graf. Na ten poslední se dnes zaměříme, ale otřeme se i o ostatní metody.

K čemu je to dobré?

Máte v plánu sledovat vývoj akcií jedné firmy. K tomu vám stačí obyčejný spojnicový graf: jednoduše identifikujete růsty a poklesy v čase nebo zhodnotíte celkový stav. Když potřebujete porovnat vývoj akcií TOP50 firem najednou, to už je v jednom spojnicovém grafu slušný nepořádek. Sáhnete pravděpodobně k metodě small multiples, kdy vytvoříte padesát spojnicových grafů, každý se stejným nastavením os a každý s jednou časovou řadou. Díky jejich vyrovnání vedle sebe teď můžete všech pět desítek firem efektivněji porovnávat, hledat výkyvy či souvislosti v jejich vývoji. Existuje však ještě efektivní rozšíření nad metodu_ small multiples_, které nám výrazně ušetří místo a zjednoduší porovnávání. Přišla s ním společnosti Panopticon, nazvala ho horizon graf a historicky navazujeme na metodu Two-Tone Pseudo Coloring (TTPC).

Jak se dělá horizon graf

Myšlenka horizon grafu spočívá v komprimaci obyčejného spojnicového, resp. plošného grafu. Začínáme běžným grafem pro jednu časovou řadu a barevně oddělujeme negativní a pozitivní hodnoty. Metoda samozřejmě stejně dobře funguje i na data bez negativních hodnot nebo při porovnávání např. vůči celonárodnímu průměru atp.

Na graf aplikujeme barevnou škálu. Využíváme divergentní (dvoukoncové) barevné stupnice: uprostřed je nula v pomyslné bílé barvě a na obě strany se pak barva skokově rozbíhá do vyšších/sytějších negativních (červených) nebo pozitivní (modrých) hodnot. Správný a efektivní počet skoků (pásků) je předmětem výzkumů, ke kterým se ještě vrátíme později.

Dalším krokem je překlopení (zrcadlení) negativních hodnot na „pozitivní” část souřadnicového systému. Variantou je tzv. offset (lze přeložit jako odsunutí), kdy negativní hodnoty posouváme na duplicitní osu umístěnou nad pozitivní hodnoty.

Samotná „komprimace” pak probíhá vrstvením jednotlivých „pásků” podle barevné škály přes sebe od nejnižších po nejvyšší. Výsledkem je horizon graf se zrcadlenými negativními hodnotami a jednou osou, nebo offset horizon graf s negativními hodnotami posunutými na samostatnou duplicitní osu.

Výhodou offsetové varianty je skutečnost, že negativní hodnoty stále klesají od osy dolů tak, jak jsme naučení grafy číst. Také se zbavujeme závislosti na barvě: nejsytější vrcholy směrem dolů jsou nejnižší negativní hodnoty a naopak. Barva tak ztrácí na důležitosti, nemusíme řešit případné potíže s barvoslepostí a nebo můžeme barvu využít ke kódování např. doplňujících kategorických informací.

Praktické využití

Nejlepší využití mají horizon grafy v již zmíněné metodě small multiples. Při seřazení jednotlivých pásků pro jednotlivé časové řady pod sebe ihned vidíme místa s největším růstem či poklesem, jejich souvislosti i případné cyklické vzory. Několik případů využití jsem vybral do galerie:

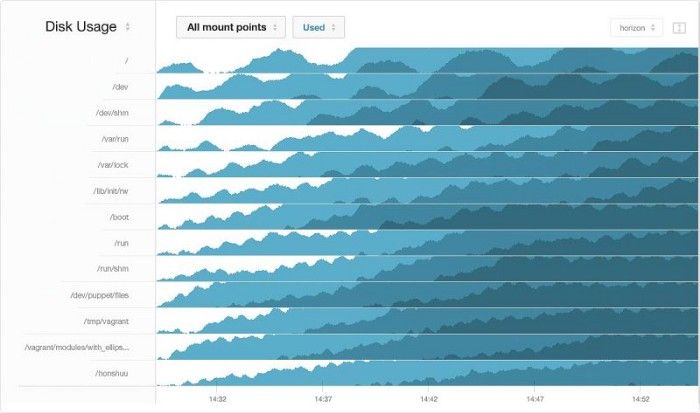
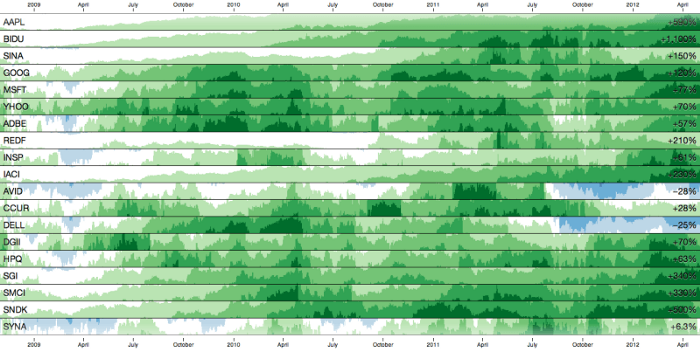
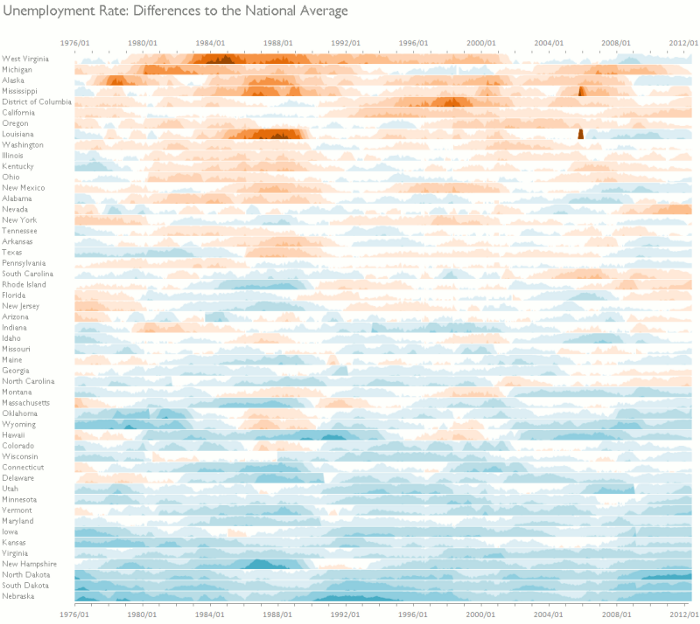
Výzkumy horizon grafů: doporučení pro praxi

Efektivitě horizon grafů se asi nejblíže věnovali Javed, McDonnel a Elmqvist, kteří se obecně zaměřili na nejrozšířenější metody statické vizualizace většího množství časových řad a podrobili je uživatelskému testování. V potaz brali a) běžný spojnicový graf s více liniemi, b) small multiples řešení s běžnými spojnicovými grafy, c) horizon grafy a d) jednu velmi okrajovou metodu nazvanou braided grafy. Ty pracují s překrývajícími se plošnými grafy (nikoliv skládanými), kde díky detekci průniků jednotlivý časových řad dochází k jejich „odkrývání” a zpřehlednění.

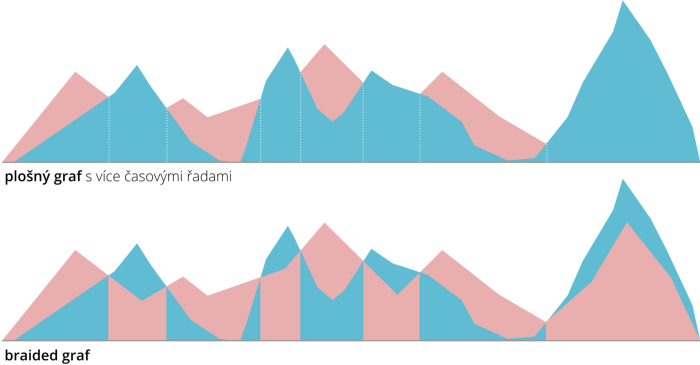
Tyto čtyři metody se liší především společným (a, d) nebo rozděleným (b, c) prostorem pro časové řady. Metody se společným prostorem (obyčejný spojnicový graf, braided graf) byly v rámci výzkumu celkem logicky efektivnější pro úkoly spojené s hledáním řady s nejvyšší hodnotou v určitém časovém bodě. Naopak grafy se samostatným prostorem pro každou řadu se ukázaly být vhodnějšími k porovnávání, což je také hlavní moment, kdy horizon graf využít: pokud chceme příjemci umožnit širší porovnávání časových řad mezi sebou i v celku.

Heer, Kong a Agrawala se pak zaměřili na otázky optimalizace poměru stran (tolik diskutovaného tématu, kdykoliv se mluví o manipulaci se spojnicovými grafy), velikosti a na některé další designově-kognitivní otázky horizon grafů. Výsledkem je několik doporučení: předně je nutné zmínit, že zrcadlení negativních hodnot do pozitivní oblasti grafu nemá žádný vliv na rychlost odhadu hodnot z grafu ani na přesnost odhadu — celkem překvapivě. Heer a spol. také radí vyvarovat se více než čtyřech pásků , které už účastníci výzkumu označovali za nečitelné. Je však vždy třeba brát v potaz kontext: chceme, aby se příjemci snažili odečítat přesné hodnoty, nebo nám jde o celkové porovnání?

V čem se to dá dělat?

Asi nejpřístupnějším nástrojem, který horizon grafy běžně podporuje je Tableu. Ačkoliv Excel přímo tento typ grafu zatím neumí, existují cesty, jak ho i tam dosáhnout (návod tady nebo tady). Interaktivní a webové horizonty umí po menším doplnění d3.js (tady nebo tady). Implementovaná je tato metoda už i ve statistickém jazyce R.

Horizon graf zatím není nijak masivně rozšířen a tak je u něj jistou bariérou „první čtení”, které od příjemce vyžaduje pozornost a pochopení konceptu. Odměnou je však možnost jednoduše vidět velké množství časových dat a ihned v nich pozorovat extrémy a vzory. Doufám, že se výhledově dočkáme jednodušších cest jeho tvorby, třeba přímo v Excelu na kliknutí. Stejně tak už ale léta očekávám i implementaci small multiples.